反比例とそのグラフ
反比例は、\(2\) つの変数 \(x,\;y\) があり、一方が他方の逆数に比例する関係をいいます。反比例
\(2\) つの変数 \(x,\;y\) があり、その関係が、 \begin{eqnarray} & &\boldsymbol{y=\frac{a}{x}}\\[7px] & &\small{\text{あるいは、}}\\[7px] & &\boldsymbol{a=xy}\;(a≠0) \end{eqnarray} で表されるとき、 \(y\) は \(x\) に反比例(はんぴれい)するといいます。また、定数 \(a\) を比例定数といいます。 比例の 場合と同じく、 \(x\) の値が変化すれば、それに対応して \(y\) の値も変化するので、 「\(\boldsymbol{y}\) は \(\boldsymbol{x}\) の関数」になります。 さらに、 \(y\) の値が変化すれば、それに対応して \(x\) の値も変わるので、 「\(x\) は \(y\) の関数」でもあります。 ここで、\(\cfrac{1}{x}=X\) とすれば、 \begin{eqnarray} y &=&\frac{a}{x}\\[7px] &=&a \times \frac{1}{x}\\[7px] &=&a \times \color{blue}{X}\\[7px] &=&\boldsymbol{aX} \end{eqnarray} この関係は、| 「\(\boldsymbol{y}\) は \(\boldsymbol{x}\) に反比例する」 | \(=\)「\(\boldsymbol{y}\) は \(\boldsymbol{\color{blue}{\cfrac{1}{x}}}\) に比例する」 |
反比例の計算
次の問題を解いてみましょう。問 題:
マサルは、お気に入りの \(CD\) を買いにとなり町まで車で行った。行きは時速 \(40km\) の速さで走って \(15\) 分かかり、 帰りは同じ道を時速 \(x\;km\) の速さで走って \(y\) 分かかった。このとき、 \(y\) を \(x\) の式で表しなさい。
速さの問題では、単位を統一します。「時間」が「時」と「分」で異なるので、ここでは「分」を「時」に変えます。また、図を使って整理するとわかりやすくなります。
\begin{align}
& 1\;\small{\text{時間は}}\;\normalsize{60}\;\small{\text{分}}\\
& \small{\text{よって、}}\\
& 15\;\small{\text{分}}\;\normalsize{=\frac{1}{4}}\;\small{\text{時間}}
\end{align}
自宅からとなり町までは、行きが時速 \(40km\) の速さで \(15\) 分進んだので、
\[40 \times \frac{1}{4}=10km\;\small{\text{ ―― ①}}\]
帰りは、時速 \(x\;km\) の速さで \(y\) 分掛けて進んだので、その距離は
\[x \times \frac{y}{60}=\frac{xy}{60}km\;\small{\text{ ―― ②}}\]
\(\small{①}\) と \(\small{②}\) は等しいので、
\begin{eqnarray}
& &\frac{xy}{60}=10\\[5px]
& &xy=600\\[5px]
& &\boldsymbol{\color{red}{y=\frac{600}{x}}}
\end{eqnarray}
この式から、
距離が一定ならば、 「かかった時間 \(\boldsymbol{(y)}\)」 は 「速さ \(\boldsymbol{(x)}\)」 に反比例することが分かります。
マサルは、お気に入りの \(CD\) を買いにとなり町まで車で行った。行きは時速 \(40km\) の速さで走って \(15\) 分かかり、 帰りは同じ道を時速 \(x\;km\) の速さで走って \(y\) 分かかった。このとき、 \(y\) を \(x\) の式で表しなさい。
反比例を表す数表
次の数表において、 \(y\) が \(x\) に反比例するとき、空所 (ア)、(イ) に当てはまる数を入れてみましょう。| \(\boldsymbol{x}\) | - | \(-2\) | - | \(0\) | - | \(2\) | - | イ | - |
|---|---|---|---|---|---|---|---|---|---|
| \(\boldsymbol{y}\) | - | \(20\) | - | \(\times\) | - | ア | - | \(5\) | - |
反比例のグラフ
例 題:
次の関数を、グラフにかいてみましょう。
反比例のグラフをかく場合、変数 \(x,\;y\) の対応表をつくり、対応する点を座標平面上に書き入れてから、その点を線で結びます。
・数表の作成
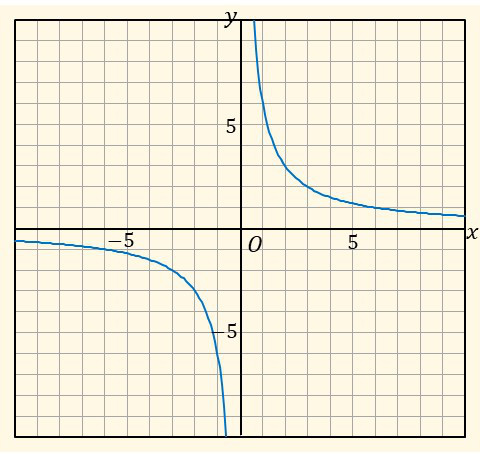
\(\boldsymbol{(1)\quad y=\cfrac{6}{x}}\)
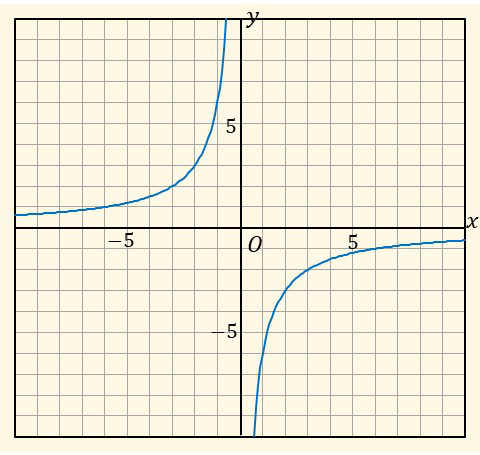
| \((1)\quad y=\cfrac{6}{x}\) | \((2)\quad y=-\cfrac{6}{x}\) |
| \(\boldsymbol{x}\) | \(-6\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(6\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\boldsymbol{y}\) | \(-1\) | \(-2\) | \(-3\) | \(-6\) | \(\times\) | \(6\) | \(3\) | \(2\) | \(1\) |
| \(\boldsymbol{x}\) | \(-6\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(6\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\boldsymbol{y}\) | \(1\) | \(2\) | \(3\) | \(6\) | \(\times\) | \(-6\) | \(-3\) | \(-2\) | \(-1\) |
 |
 |
グラフから式を求める
例 題:
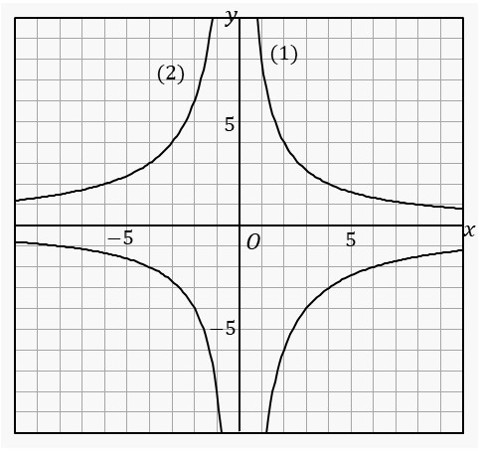
\((1),\;(2)\) のグラフになる関数は、次のどれかを答えましょう。
\((1),\;(2)\) のグラフになる関数は、次のどれかを答えましょう。
| ア \(y=\cfrac{4}{x}\) | イ \(y=\cfrac{8}{x}\) |
| ウ \(y=-\cfrac{12}{x}\) | エ \(y=-\cfrac{8}{x}\) |
 |
| \(\small{①}\) | グラフ内の座標 \(\boldsymbol{(x,\hspace{9px}y)}\) のうち整数のものを求める |
| \(\small{②}\) | \(\small{①}\) から比例定数 \(\boldsymbol{a}\) を求める |
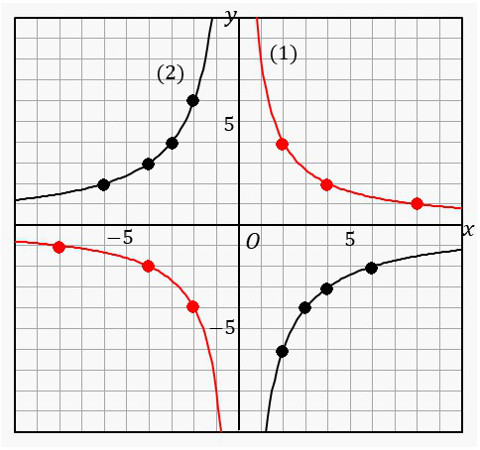 |
| \(\boldsymbol{x}\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(1\) | \(2\) | \(4\) | \(8\) |
|---|---|---|---|---|---|---|---|---|
| \(\boldsymbol{y}\) | \(-1\) | \(-2\) | \(-4\) | \(-8\) | \(8\) | \(4\) | \(2\) | \(1\) |
| \(\boldsymbol{xy=a}\) | \(8\) | \(8\) | \(8\) | \(8\) | \(8\) | \(8\) | \(8\) | \(8\) |
| \(\boldsymbol{x}\) | \(-6\) | \(-4\) | \(-3\) | \(-2\) | \(2\) | \(3\) | \(4\) | \(6\) |
|---|---|---|---|---|---|---|---|---|
| \(\boldsymbol{y}\) | \(2\) | \(3\) | \(4\) | \(6\) | \(-6\) | \(-4\) | \(-3\) | \(-2\) |
| \(\boldsymbol{xy=a}\) | \(-12\) | \(-12\) | \(-12\) | \(-12\) | \(-12\) | \(-12\) | \(-12\) | \(-12\) |
| \(∴\quad\boldsymbol{a=-12(1)}\):イ \(\boldsymbol{(2)}\):ウ |