方程式とその解
文字を含む式のうち、その文字に特定の数を入れたときにだけ成立するものを方程式といいます。方程式を解くには、等式の性質を利用します。| ・方程式の意味とその解について |
| ・方程式の解き方をマスターする |
| ・方程式の文章問題 解き方のコツについて |
| この項目についてお聞きになりたいことは、「*ご質問・お問わせ」からお願いします |
方程式
\(1+2=3\) のように、すでに成立している等式とは違って、 \(2x+5=0,\quad2x+3=3x+7\) のように、文字を含む式は、その文字に入る値によって成立する場合もあれば、成立しない場合もあります。このように、文字を含み、その文字に特定の数字を入れたときにだけ成り立つ式を方程式(ほうていしき)といいます。\(2x+5=0\) のように、文字が「\(x\)」のときには、「\(\boldsymbol{x}\) についての方程式」といい、文字が \(a\) のときには、「\(\boldsymbol{a}\) についての方程式」といいます。 \(x\) についての方程式において、その方程式を成り立たせる \(x\) の値をその方程式の「解」(かい) といい、 ことばの意味
| 方 程 式 | 文字を含む式のうち、その文字に特定の数を入れたときにだけ成立するもの |
|---|
等式の性質 \(\boldsymbol{1}\)
\begin{eqnarray} & & \boldsymbol{A=B}\\[5px] & & \small{\text{ならば}}\\[5px] & & \boldsymbol{\color{blue}{A+C=B+C}} \end{eqnarray} \(1\) 個 \(10g\) のおもり ○ と、 \(1\) 個 \(15g\) のおもり \(△\) があるとしましょう。 これらをてんびんに乗せてつり合うようにするため には、 \(10g\) のおもりを \(3\) 個 (○○○) と、 \(15g\) のおもり \(2\) 個〈△△〉にすれば、どちらも \(30g\) で同じになります。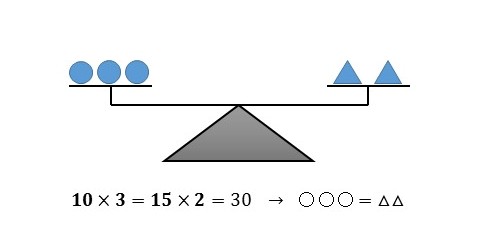 |
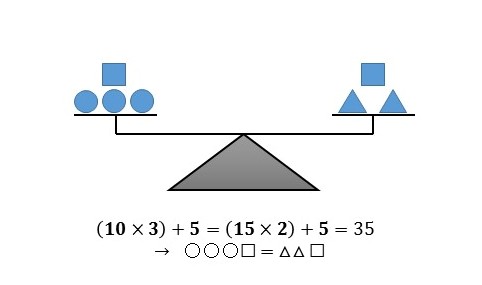 |
| 「ある等式 \((A=B)\) の両辺に、同じ数量 \((C)\) を | 加えても、その等式は成り立つ」 |
「方程式を解く」とは、方程式を成り立たせる文字の値を求めることですから、 \[\color{blue}{x=(\quad)}\] の形に式を変えることをいいます。 \(x-9=3\) の場合、左辺の \(-9\) を省かなければならなりません。 それには、 式の両辺に \((+9)\) を加えれば \((-9)\) は消去されます。 \begin{eqnarray} & & x+(-9)\color{red}{+(+9)}\\[5px] & & \hspace{10px}=3\color{red}{+(+9)}\\[5px] & & \boldsymbol{x=12} \end{eqnarray} このようにして、 \(x\) の値が割り出せます。
次に、 \(x=12\) が本当に方程式の解として正しいかを、もとの方程式の \(x\) に「\(12\)」を代入して確かめます。 \begin{eqnarray} & & x-9=3\\[5px] & & \small{\text{において、}}\\[5px] & & \small{\text{左辺}}\normalsize{=12-9=3}\\[5px] & & \small{\text{右辺}}\normalsize{=3} \end{eqnarray} 「左辺」\(=\)「右辺」となり、この方程式の解は \(12\) であると確認できます。
等式の性質 \(\boldsymbol{2}\)
\begin{eqnarray} & & A=B\\[5px] & & \small{\text{ならば}}\\[5px] & & \boldsymbol{\color{blue}{A-C=B-C}} \end{eqnarray} 等式の性質 \(1\) の逆になります。 \(1\) 個 \(10g\) のおもり ○ が \(3\) 個に \(1\) 個 \(5g\) のおもり \(□\) が \(1\) 個てんびんの左の皿に乗り、 右の皿には、 \(15g\) のおもり \(△\) が \(2\) 個と \(5g\) のおもり \(□\) が \(1\) 個が乗ってつり合っています。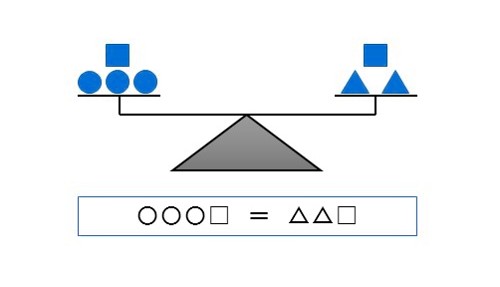 |
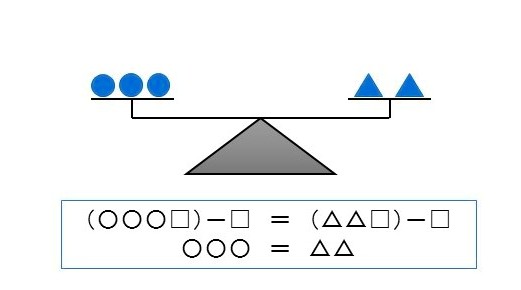 |
| 「ある等式 \((A=B)\) の両辺から、同じ数量 \((C)\) | を引いてても、その等式は成り立つ」 |
方程式の解を求めるには \(\color{blue}{x=(\quad)}\) の形にしますから、左辺の \((+12)\) を取り除きます。 \begin{eqnarray} & & x+12=-5\;\small{\text{の両辺に}}\\[5px] & & (-12)\;\small{\text{を加えて、}}\\[5px] & & x+12\color{red}{+(-12)}=-5\color{red}{+(-12)}\\[5px] & & x=-(5+12)=-17 \end{eqnarray} 次に、\(x=-17\) がこの方程式の解として正しいかを確認します。もとの方程式の \(x\) に \(-17\) を代入して、 \begin{eqnarray} & & \small{\text{左辺}}\normalsize{=x+12}\\[5px] & & \hspace{16px}=(-17)+12\\[5px] & & \hspace{16px}=-(17-12)=-5\\[5px] & & \small{\text{右辺}}\normalsize{=-5} \end{eqnarray} よって、
\(\boldsymbol{x=-17}\) が方程式の解になります。
等式の性質 \(\boldsymbol{3}\)
\begin{eqnarray} & & \boldsymbol{A=B}\\[5px] & & \small{\text{ならば}}\\[5px] & & \boldsymbol{\color{blue}{A \times C=B \times C}} \end{eqnarray} てんびんの左の皿には \(1\) 個 \(10g\) のおもり ○ が \(3\) 個、右の皿には、\(1\) 個 \(15g\) のおもり \(△\) が \(2\) 個乗ってつり合っています。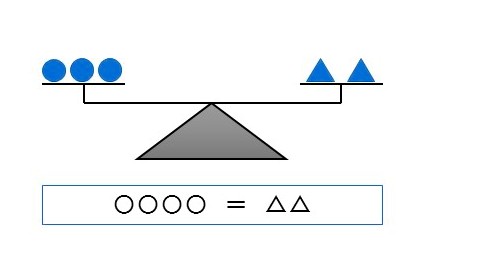 |
| ○○○\(+\)○○○ \(\gt\) △△ |
 |
| 「ある等式 \((A=B)\) の両辺に、同じ数量 \((C)\) を | 掛けても、その等式は成り立つ」 |
等式の性質 \(\boldsymbol{4}\)
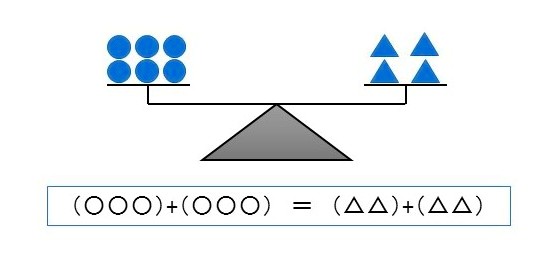
\begin{eqnarray} & & \boldsymbol{A=B}\\[5px] & & \small{\text{ならば }}\\[5px] & & \boldsymbol{\color{blue}{A \div C=B \div C}} \end{eqnarray} 等式の性質 \(3\)〈乗法〉の逆になります。左右のおもりをそれぞれ半分ずつにしても元に戻るだけだからてんびんはつり合います。(○○○)(○○○) \(=\) (△△)(△△) ならば、 \[\color{crimson}{\cfrac{(○○○)(○○○)}{○○○}=\cfrac{(△△)(△△)}{△△}}\]
| 「等式 \((A=B)\) の両辺を同じ数 \((C)\) で割っても、 | 等式は成り立つ」 |
\(6x\) の \(6\) を取り除くためにその逆数 \(\color{blue}{\cfrac{1}{6}}\) を式の両辺に掛けると、 \begin{eqnarray} & & 6x=48\\[5px] & & 6x \color{red}{\times \frac{1}{6}}=48x \color{red}{\times \frac{1}{6}}\\[5px] & & x=8 \end{eqnarray} という答えが出ます。次に、 \(x=8\) が方程式の解として正しいかを確認するために、もとの方程式の \(x\) に \(8\) を代入します。 \begin{eqnarray} & & \small{\text{左辺}}\; \normalsize{=6 \times 8=48}\\[5px] & & \small{\text{右辺}}\; \normalsize{=48} \end{eqnarray} このように、左辺と右辺が一致するから、 \(x=8\) がこの方程式の解として正しいと確認できました。除法は乗法に変えて、「等式の両辺に同じ数の逆数を掛けても、等式は成り立つ」を利用する方が計算が楽に行えます。