直線と平面の位置関係
空間内における直線と直線、直線と平面、平面と平面 それぞれの位置関係について、・空間内の \(2\) 直線の位置関係は、「交わる」「平行」「ねじれの位置」の \(3\) 通り ・空間内の \(2\) 平面の位置関係は、「交わる」「平行」の \(2\) 通り ・空間内の 直線と平面の位置関係は、「交わる」「平行」「直線が平面に含まれる」の \(3\) 通りが考えられます。\(\boldsymbol{2}\) 直線の位置関係
空間における、\(2\) つの直線の位置関係には、次の \(\boldsymbol{3}\) つが考えられます。 \(\small{①}\) 同じ平面上にあって交わる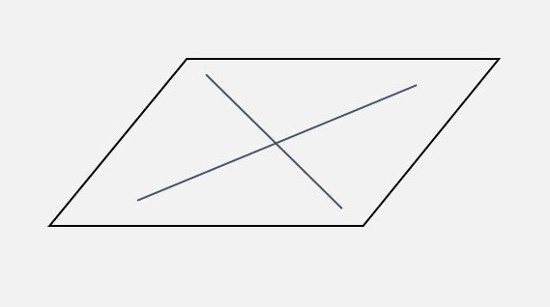 |
 |
 |
 |
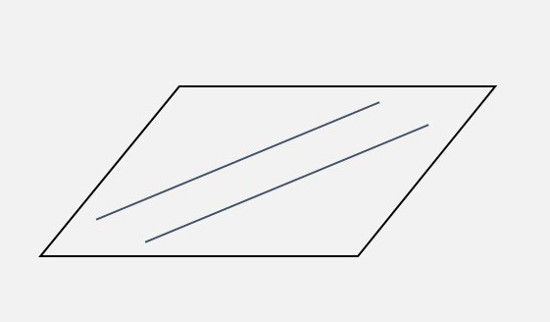
| \((1)\) 平行である |
| \((2)\) 垂直に交わる |
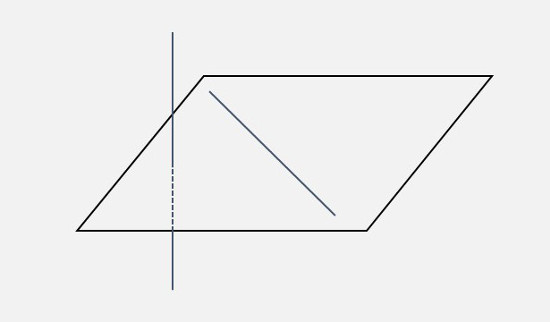
| \((3)\) ねじれの位置にある |
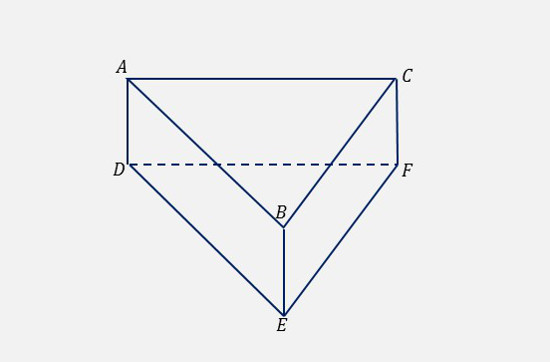
同じ平面上にあるものは、面 \(\boldsymbol{ABED}\) 上の辺 \(\boldsymbol{BE}\) と、面 \(\boldsymbol{ACFD}\) 上の辺 \(\boldsymbol{CF}\) \[\boldsymbol{∴\quad \color{blue}{\small{\text{辺}}\;\normalsize{BE,\;CF}}}\] \(\boldsymbol{(2)}\) 辺 \(\boldsymbol{AD}\) と垂直に交わる辺
\(8\) つの辺の中で、辺 \(AD\) と交わる辺は、 辺 \(\boldsymbol{AB,\;AC,\;DE,\;DF}\) で、すべてが垂直に交わる \[\boldsymbol{∴\quad \color{blue}{\small{\text{辺}}\;\normalsize{AB,\;AC,\;DE,\;EF}}}\] \(\boldsymbol{(3)}\) 辺 \(\boldsymbol{AD}\) とねじれの位置にある辺
「どこまで延ばしても交わらない」 辺 \(BE,\;CF,\;BC,\;EF\) の \(4\) つのうち、\(2\) つの 辺 \(\boldsymbol{BC,\;EF}\) が同じ平面上にない \[\boldsymbol{∴\quad \color{blue}{\small{\text{辺}}\;\normalsize{BC,\;EF}}}\]
直線と平面の位置関係
直線と平面の位置関係には、次の \(3\) つが考えられます。\(\small{①}\) \(\boldsymbol{1}\) 点で交わる
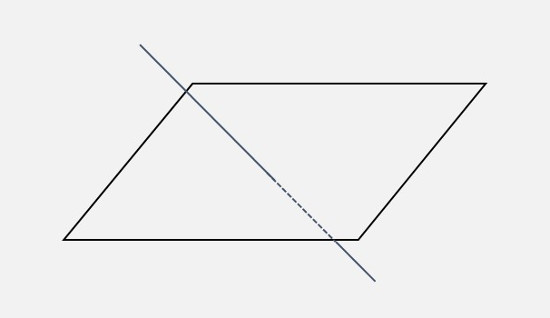 |
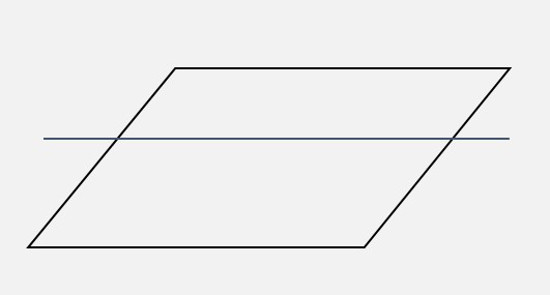 |
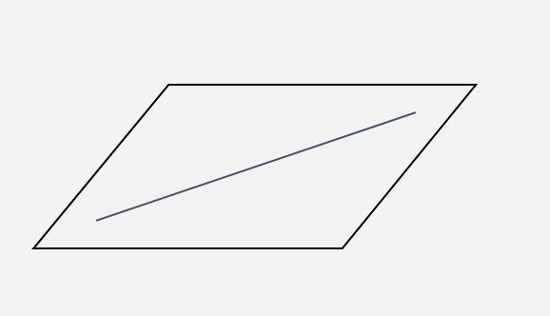 |
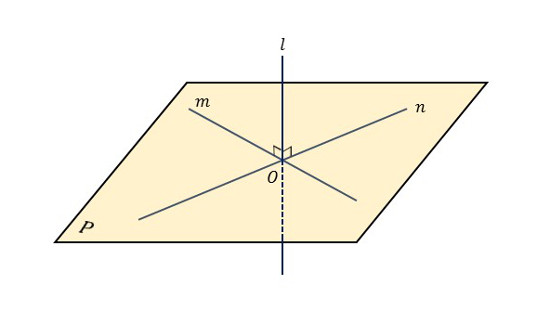 |
| \(\boldsymbol{直線\;\large{l ⊥ }\normalsize{平面}\;\large{P}}\) |
 |
| \(\boldsymbol{点\;\large{P}\;\normalsize{と平面との距離}}\) |
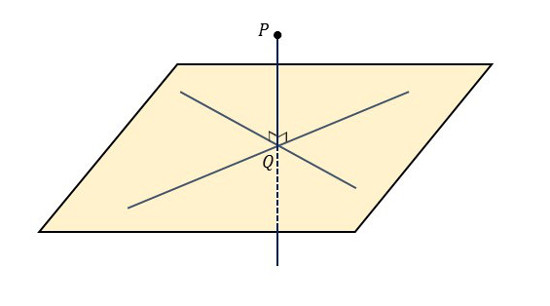 |
例 題
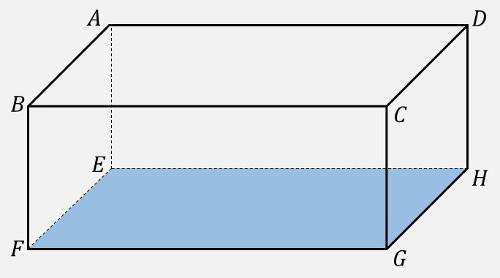
次のような直方体があるとき、下の質問に答えてみましょう。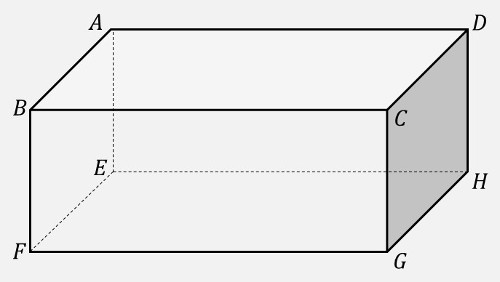 |
面を表現するとき、その面のある \(1\) つの頂点 (この場合 \(A\)) を基準にして、反時計(左)回りか時計(右)回りに \(1\) 周するように記号名を述べます。
\[\boldsymbol{\small{\text{面}}\;\normalsize{ABCD}\small\;{\text{と面} }\;\normalsize{ABFE}}\]
\(\boldsymbol{(2)}\) 辺 \(\boldsymbol{AB}\) と垂直な面は \(\boldsymbol{?}\)
面を考える前に辺 \(\boldsymbol{AB}\) と垂直な辺を考えてから、その辺を含む面を考えるようにします。 辺 \(AB\) と垂直な辺は、辺 \(\boldsymbol{AD,\;BC,\;AE,\;BF}\) の \(4\) つになります。 辺 \(AB\) と \(4\) つの辺のうちの \(2\) つの辺をを含む面があれば、それが辺 \(AB\) と垂直な面となります。
\[\boldsymbol{\small{\text{面}}\;\normalsize{ADHE}\small\;{\text{と 面}}\;\normalsize{BCGF}}\]
\(\boldsymbol{(3)}\) 辺 \(\boldsymbol{AB}\) と平行な面は \(\boldsymbol{?}\)
辺 \(AB\) と平行な面は、この辺とどこまで延ばしても交わらない面になります
\[\boldsymbol{\small{\text{面}}\;\normalsize{CGHD}\small\;{\text{と 面}}\;\normalsize{EFGH}}\]
\(\boldsymbol{(4)}\) 面 \(\boldsymbol{ABCD}\) と垂直な辺は \(\boldsymbol{?}\)
面 \(ABCD\) と垂直な辺は、面 \(ABCD\) 上にある辺と垂直な辺のことです。
| 面 \(ABCD\) 上の辺 \(\boldsymbol{AB}\) と垂直な辺 | ⇒ 辺 \(\boldsymbol{AE}\) と \(\boldsymbol{BF}\) |
| 面 \(ABCD\) 上の辺 \(\boldsymbol{BC}\) と垂直な辺 | ⇒ 辺 \(\boldsymbol{BF}\) と \(\boldsymbol{CG}\) |
| 面 \(ABCD\) 上の辺 \(\boldsymbol{CD}\) と垂直な辺 | ⇒ 辺 \(\boldsymbol{CG}\) と \(\boldsymbol{DH}\) |
| 面 \(ABCD\) 上の辺 \(\boldsymbol{DA}\) と垂直な辺 | ⇒ 辺 \(\boldsymbol{DH}\) と \(\boldsymbol{AE}\) |
面 \(ABCD\) とどこまで延ばしても交わらない辺になります。 \begin{eqnarray} & &\boldsymbol{\color{blue}{\small{\text{辺}}\;\normalsize{EF,} \qquad \small{\text{辺}}\;\normalsize{FG,}}}\\[5px] & &\boldsymbol{\color{blue}{\small{\text{辺}}\;\normalsize{GH,}\qquad \small{\text{辺}}\;\normalsize{EH}}}\;\small{\text{ … 答え}} \end{eqnarray}
\(\boldsymbol{2}\) つの平面の位置関係
空間内の \(2\) つの平面の位置関係は、次の \(2\) つ。① 交わる
 |
 |
\[\boldsymbol{m⊥n\;\small{\text{ならば}}\;\normalsize{P⊥Q}}\]
が成り立ちます。
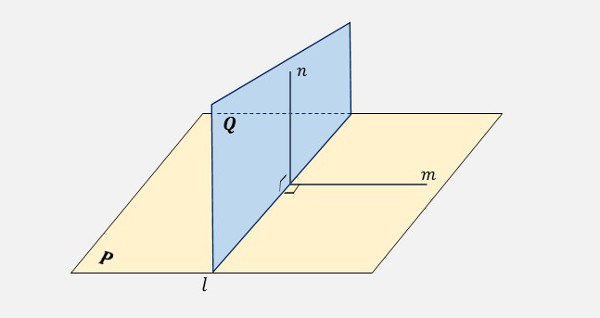 |
 |
面 \(ABCD\) の各辺を他の平面との交線と考えます。
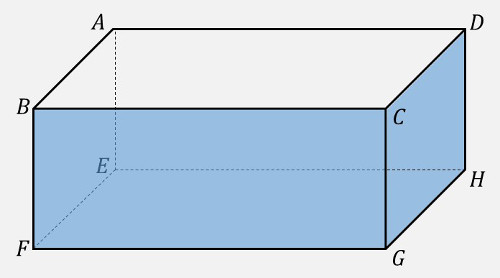 |
\begin{eqnarray}
& &\small{\text{面}}\;\normalsize{ABFE,}\qquad \small{\text{面}}\;\normalsize{BCGF,}\\[5px]
& &\small{\text{面}}\;\normalsize{CDHG,}\qquad
\small{\text{面}}\;\normalsize{DAEH}\;\small{\text{… 答え}}
\end{eqnarray}
\(\boldsymbol{(2)}\) 面 \(\boldsymbol{ABCD}\) と平行な面は \(\boldsymbol{?}\)
面 \(ABCD\) と平行な面は、その面をどこまで延ばしても交わらないものをいいます。
 |