確率の求め方
あることがらが起こる確率を求める実験をする場合、\(1\) 回や \(2\) 回の実験では、どの程度そのことがらが起こるのかを正確に判断できません。そのため、実験には十分な回数が必要になります。確 率
ある出来事が起こる可能性の大きさを表す数値のことを確率(かくりつ) といいます。確率は、すべての出来事やことがらに対するその出来事やことがらの起こる割合なので、ある出来事の起こる確率を \(p\) とし、その出来事の起こる回数を \(a,\) すべての 出来事の起こる回数を \(n\) とすると、 \[\boldsymbol{p}=\cfrac{\color{blue}{a}}{\color{blue}{n}}\] で求めることができます。たとえば、一定の条件で実験をくり返したところあることがら起こったとすると、| 実験を \(\boldsymbol{\color{blue}{n}}\) 回くり返すとある事柄が \(\boldsymbol{\color{blue}{a}}\) 回起こる |
| ・ | \(\boldsymbol{1}\) 枚のコインを投げて何回表が出たかを記録する |
| ・ | これを \(\boldsymbol{100}\) 回くり返し合計 \(\boldsymbol{1000}\) 回投げる |
| ・ | 表が出た回数と割合を \(\boldsymbol{10}\) 回ごとに算出する |
| ・ | それをグラフにする |
| 投げた回数 | \(100\) | \(200\) | \(300\) | \(400\) | \(500\) | \(600\) | \(700\) | \(800\) | \(900\) | \(1000\) |
| 表が出た回数 | \(51\) | \(100\) | \(145\) | \(190\) | \(237\) | \(287\) | \(340\) | \(396\) | \(447\) | \(491\) |
| 表が出た割合 | \(\boldsymbol{0.51}\) | \(\boldsymbol{0.50}\) | \(\boldsymbol{0.48}\) | \(\boldsymbol{0.48}\) | \(\boldsymbol{0.47}\) | \(\boldsymbol{0.48}\) | \(\boldsymbol{0.49}\) | \(\boldsymbol{0.50}\) | \(\boldsymbol{0.50}\) | \(\boldsymbol{0.49}\) |
| (表が出た割合) | \(=\) (表が出た回数) \(\div\) (コインを投げた回数) |
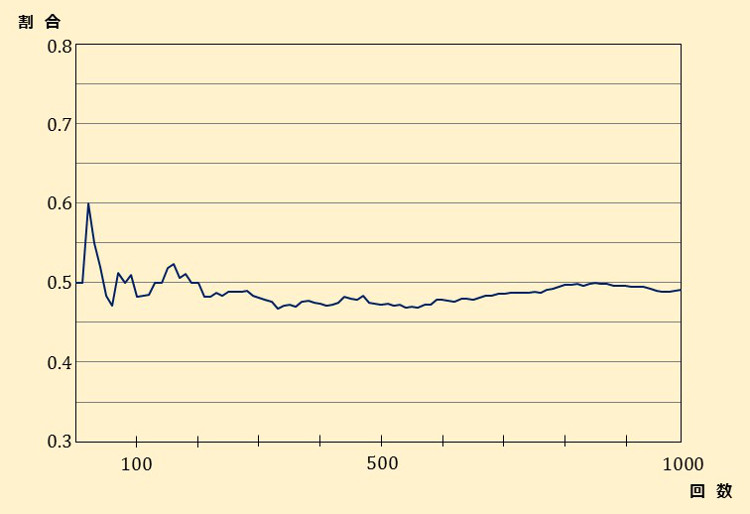 |
| コインを \(\boldsymbol{1000}\) 回投げて、 | 表が出る確率は \(\boldsymbol{0.5\;(\cfrac{1}{2})}\) である |
確率の求め方
上の例題で取り上げた、「コインを投げて表が出る確率」を計算で求める方法について学習します。| \(\small{①}\) | コインを投げたときに出る面は、表と裏の \(\boldsymbol{2}\) 通り |
| \(\small{②}\) | 一方の面にかたよった出方をせず、どちらの面が出るのも同じ程度に期待される |
| \(\small{③}\) | \(\boldsymbol{2}\) 通りの出方のうち、表が出るのは \(\boldsymbol{1}\) 通り |
確率を求める場合、起こる場合の数が全部で \(\boldsymbol{n}\) 通りあり、どの事柄が起こるのも同様に確からしいとします。 そのうち、ある出来事の起こる確率を \(\boldsymbol{p}\), その出来事の起こる回数を \(\boldsymbol{a}\) とすれば、 \[\boldsymbol{p}=\cfrac{\color{blue}{a}}{\color{blue}{n}}\] が成り立ちます。上の例題では、 \(\boldsymbol{n=2,\;a=1}\) ですから 表が出る確率 \[p=\cfrac{1}{2}\] 事柄が絶対に起こらないとき、起こる確率は \[\boldsymbol{p=\cfrac{0}{n}=0}\] であり、事柄が必ず起こるとき、起こる確率は \[\boldsymbol{p=\cfrac{n}{n}=1}\] このときの確率 \(\boldsymbol{p}\) の範囲は \[\boldsymbol{\color{blue}{0 ≦ p ≦ 1}}\] となります。
| \(\boldsymbol{2}\) 個のサイコロを同時に投げたとき、 | 出る目の和が \(\boldsymbol{4}\) の倍数となる確率 |
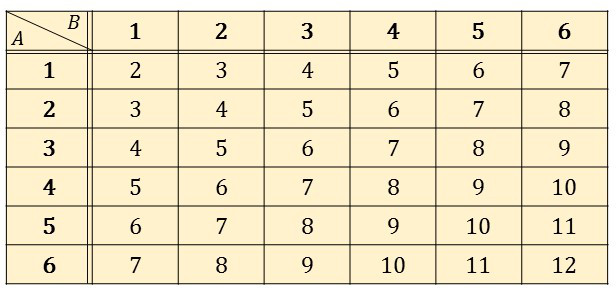 |
| \(\boldsymbol{6 \times 6=36}\) (通り) |
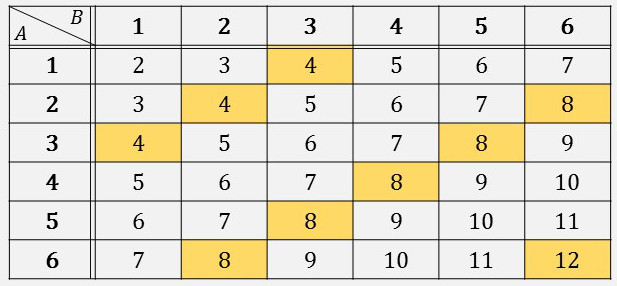 |
| 出る目の和が \(\boldsymbol{4}\) の倍数となる場合の数 \(=\) \(\boldsymbol{\color{blue}{9}}\) (通り) |