高校入試[英語・数学]| 三平方の定理：重要問題

重要問題

三平方の定理は、直角三角形に用いることができます。そのため、定理の利用には直角三角形を探したり、補助線を引いて直角三角形をつくります。また、空間図形を切断したり、展開することで平面図形をうまく利用して高さを求めます。

三平方の定理の証明

問　題
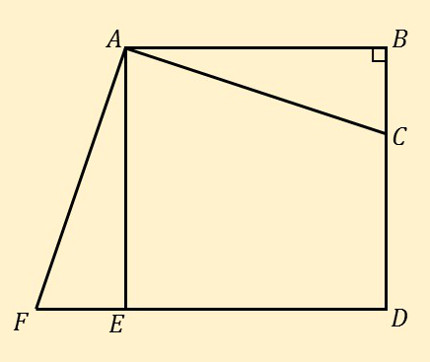
\(∠B\) が直角である直角三角形 \(ABC\) において、 \(AC=\boldsymbol{a},\quad AB=\boldsymbol{b},\quad BC=\boldsymbol{c}\)　とする。 \(AB\) を \(1\) 辺とする正方形 \(ABDE\) を図のようにつくり、辺 \(DE\) の延長線上に \(EF=BC\) となる点 \(F\) をとるとき、次の問いに答えなさい。

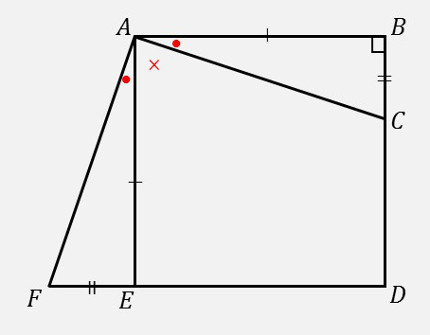
\((1)\)	\(∠FAC\) が直角であることを証明しなさい。
\((2)\)	四角形 \(ACDF\) の面積が、正方形 \(ABDE\) の面積に等しいことを証明しなさい。
\((3)\)	\((2)\) を用いて、三平方の定理 \(a^2=b^2+c^2\) が成り立つことを証明しなさい。

解　説

\(\boldsymbol{(1)} \quad △ABC ≡ △AEF\) であることを証明します

証　明 \begin{eqnarray} & &△ABC\;\small{と}\;\normalsize{△AEF}\;\small{において、}\\[5px] & &\small{仮定より、}\\[5px] & &\boldsymbol{AB=AE}\;――\;1\\[5px] & &\boldsymbol{BC=EF}\;――\;2\\[12px] & &∠ABC=∠AED=90^{\circ}\\[5px] & &\small{より、}\\[12px] & &∠AEF=∠DEF-∠AED\\[5px] & &\hspace{14px}=180-90\\[5px] & &\hspace{14px}=\boldsymbol{90^{\circ}}\;――\;3\;\small{\color{red}{(∠DEF\;は直線の角)}}\\[12px] & &1\;\sim\;3\;\small{より、} \end{eqnarray} \(2\) 辺とその間の角がそれぞれ等しい \(2\) つの三角形は合同であるから、 \[\boldsymbol{△ABC ≡ △AEF}\;――\;4\] 合同な図形の対応する角はすべて等しいので、 \begin{eqnarray} & &∠FAE=∠CAB\;――\;5\\[12px] & &∠BAE=∠CAB+∠EAC\\[5px] & &\hspace{14px}=90^{\circ}\\[5px] & &5\;\small{より、}\\[12px] & &∠FAC=∠FAE+∠EAC\\[5px] & &\hspace{14px}=\boldsymbol{90^{\circ}} \end{eqnarray}

よって、\(\boldsymbol{∠FAC}\) は直角である　…　証明終わり

\(\boldsymbol{(2)}\)　証　明

\begin{eqnarray} & &(1)\;\small{より、}\\[5px] & &\boldsymbol{△ABC}\;\small{\mathbf{の面積}}\;\normalsize{\boldsymbol{=△AEF}}\;\small{\mathbf{の面積}}\;\normalsize{――\;1}\\[5px] & &\small{\mathbf{正方形}}\;\normalsize{\boldsymbol{ABDC}}\;\small{\mathbf{の面積}}\\[5px] & &=\boldsymbol{△ABC+□ACDE}\;\small{\mathbf{の面積}}\;\normalsize{――\;2} \end{eqnarray} よって、
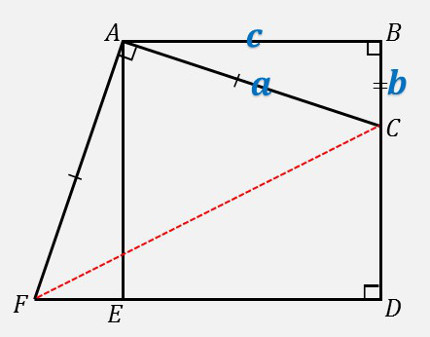
\(\boldsymbol{△AEF+□ACDE}\;\)の面積 \(=\) 正方形 \(\boldsymbol{ABDC}\) の面積が成り立つ　…　証明終わり

\(\boldsymbol{(3)}\)　証　明

四角形 \(ACDF\) に補助線として対角線 \(CF\) を引きます \begin{eqnarray} & &(2)\;\small{より、}\\[5px] & &\small{\mathbf{正方形}}\;\normalsize{\boldsymbol{ABDC}}\;\small{\mathbf{の面積}}\;\normalsize{=\boldsymbol{□ACDF}\;――\;1}\\[12px] & &\normalsize{□ACDF}\;\small{に対角線}\;\normalsize{CF}\;\small{を引くと、}\\[12px] & &\normalsize{□ACDF}\;\small{の面積}\;\normalsize{=△FAC+△CDF}\;\small{の面積}\\[5px] & &=\;\small{正方形}\;\normalsize{ABDE}\;\small{の面積\;より、} \end{eqnarray}

\[\boldsymbol{\color{crimson}{\frac{1}{2} \times a \times a+\frac{1}{2} \times (b+c)(c-b)=c^2}}\] が成り立つので、これを整理して、 \begin{eqnarray} & &\frac{1}{2}a^2+\frac{1}{2}(b+c)(c-b)=c^2\\[7px] & &\small{両辺に}\;\normalsize{2}\;\small{を掛けて、}\\[7px] & &a^2+(b+c)(c-b)=2c^2\\[5px] & &a^2+bc-b^2+c^2-bc=2c^2\\[5px] & &a^2-b^2+c^2=2c^2\\[5px] & &a^2=2c^2+b^2-c^2\\[5px] & &\boldsymbol{\color{blue}{a^2=b^2+c^2}} \end{eqnarray} よって、直角三角形 \(ABC\) において、
直角をはさむ \(\boldsymbol{2}\) 辺 \(\boldsymbol{b,\;c}\) の \(2\) 乗の和が斜辺 \(a\) の \(\boldsymbol{2}\) 乗に等しくなるので、
三平方の定理 \(\boldsymbol{a^2=b^2+c^2}\) が成り立つ
　…　証明終わり

三角形の \(\boldsymbol{3}\) 辺の長さから面積を求める

問　題
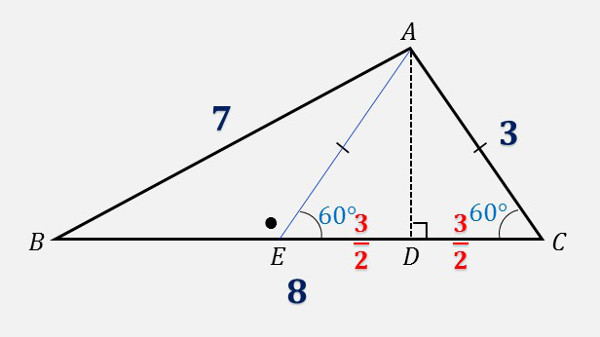
\(1\) 辺の長さがそれぞれ、\(AB=7\;cm, \quad BC=8\;cm, \quad CA=3\;cm\) の \(△ABC\) において、次の問いに答えなさい。

\((1)\)	頂点 \(A\) から辺 \(BC\) へ下した垂線と \(BC\) との交点を \(D\) とするとき、\(BD\) の長さを答えなさい。
\((2)\)	\(△ABC\) の面積を答えなさい。
\((3)\)	\(∠C\) の大きさを答えなさい。
\((4)\)	三角形の \(1\) つの内角が \(120^{\circ}\) であり、 \(3\) 辺の長さがすべて整数である場合、このような三角形の \(3\) 辺の長さの組を \(1\) つ答えなさい。

解　説
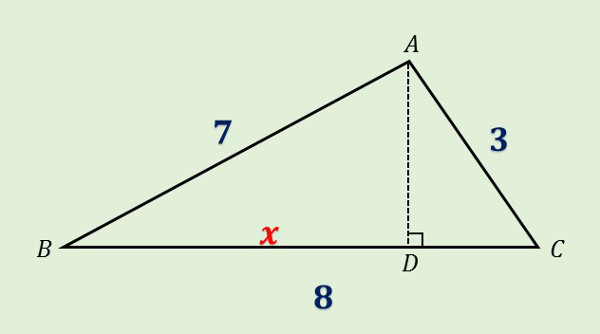
\(\boldsymbol{(1)}\)　\(BD=x\) として三平方の定理を利用します

\begin{eqnarray} & &BD=x\;\small{として、}\\[5px] & &AD^2=AB^2-BD^2,\\[5px] & &AD^2=CA^2-CD^2\;\small{より、}\\[12px] & &(7)^2-x^2=(3)^2-(8-x)^2\;\small{から、}\\[5px] & &\small{これを解き}\\[5px] & &49-x^2\\[5px] & &=9-(64-16x+x^2)\\[12px] & &-x^2+x^2-16x=9-64-49\\[7px] & &-16x=-104\\[7px] & &x=\frac{104}{16}\\[7px] & &\hspace{12px}=\frac{13}{2}\\[12px] & &\boldsymbol{∴\quad BD=\frac{13}{2}\;cm}\;…\;答え \end{eqnarray}

\(\boldsymbol{(2)}\) \begin{eqnarray} & &(1)\;\small{より、}\\[9px] & &AD=\sqrt{49-\left(\frac{13}{2} \right)^2}\\[9px] & &\hspace{7px}=\sqrt{49-\frac{169}{4}}\\[9px] & &\hspace{7px}=\sqrt{\frac{196}{4}-\frac{169}{4}}\\[9px] & &\hspace{7px}=\sqrt{\frac{27}{4}}\\[9px] & &\hspace{7px}=\frac{3\sqrt{3}}{2}\;cm\\[9px] & &△ABC=\frac{1}{2} \times 8 \times \frac{3\sqrt{3}}{2}\\[9px] & &\hspace{7px}=\boldsymbol{6\sqrt{3}\;cm^2} \end{eqnarray}

\(\boldsymbol{(3)}\) \begin{eqnarray} & &△ACD\;\small{において、}\\[5px] & &CD:AC:AD=1:2:\sqrt{3}\;\small{より、}\\[5px] & &30^{\circ},\;60^{\circ},\;90^{\circ}\;\small{の直角三角形}\\[5px] & &\small{になります}\\[12px] & &\boldsymbol{∴ \quad ∠C=60^{\circ}}\;…\;答え \end{eqnarray}

\(\boldsymbol{(4)}\)　問題の \(△ABC\) を利用します \(△ABC\) において、\(∠AEC=60^{\circ}\) になるような線分 \(AE\) を引くと、 \begin{eqnarray} & &△ABE\;\small{において、}\\[5px] & &∠AEB=180-60\\[5px] & &=\boldsymbol{120^{\circ}} \end{eqnarray} このとき、 \(△AEC\) は \(1\) 辺が \(3\;cm\) の正三角形なので、 \begin{eqnarray} & &AE=\boldsymbol{3\;cm}\;――\;1\\[5px] & &BE=8-3\\[5px] & &\hspace{29px}=\boldsymbol{5\;cm}\;――\;2\\[5px] & &\boldsymbol{∴\quad 3}\;\mathbf{\small{辺の長さの組}}\\[5px] & &\hspace{29px}=\boldsymbol{3\;cm,5\;cm,7\;cm}\;…\;答え \end{eqnarray}